
Theory and description of the experiment
 We are working to measure turbulent dissipation fluctuations using a new laser and imaging technique. Turbulent dissipation is the viscous conversion of mechanical energy to heat. Imagine putting energy into a fluid system by dragging your hand through it. Behind your hand, you see circular vortices forming. These vortices spin off smaller vortices which in turn spin off even smaller vortices. In this cascade, kinetic energy is carried down to smaller and smaller scales. At a particular scale, viscosity smooths out the flow, stopping the cascade and converting the mechanical energy to heat. When you stop moving your hand, the energy dissipation quickly stops the fluid motion. This process plays a central role in modeling and understanding turbulent flows. However, no direct measurement of the full 3-dimensional local dissipation has ever been made.
We are working to measure turbulent dissipation fluctuations using a new laser and imaging technique. Turbulent dissipation is the viscous conversion of mechanical energy to heat. Imagine putting energy into a fluid system by dragging your hand through it. Behind your hand, you see circular vortices forming. These vortices spin off smaller vortices which in turn spin off even smaller vortices. In this cascade, kinetic energy is carried down to smaller and smaller scales. At a particular scale, viscosity smooths out the flow, stopping the cascade and converting the mechanical energy to heat. When you stop moving your hand, the energy dissipation quickly stops the fluid motion. This process plays a central role in modeling and understanding turbulent flows. However, no direct measurement of the full 3-dimensional local dissipation has ever been made.
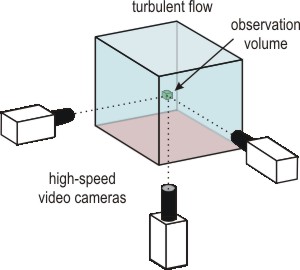
The shear flow which we are studying is set up in a square tank by one of two methods. The first is Rayleigh-Benard convection in which the bottom of the tank is heated while the top is cooled. The turbulent flow in this case displays localized "winds" of high-velocity fluid in a much slower moving fluid background. The second method we use to produce turbulence is an oscillating grid. In this set-up, a grid oscillates vertically in the fluid, setting up homogeneous turbulence throughout the tank. The turbulent flow in either case is related to the Reynolds number Re of the system, which one can calculate: Re=ul/ν, where u is the characteristic speed of the fluid, l is the height of the tank in the case of convection flow (24 cm) and the size of the grid in the second case, and ν is the viscosity of the fluid (ν=0.01 cm2/s for water). At sufficiently high Re, the flow is turbulent.
We are looking at the turbulence at small scales (on the order of 1 mm). To do so, we seed the flow with small spherical particles which are 20 μm. The particles are illuminated with a 5 W laser and observed from three perpendicular directions by three high-speed (up to 8000 frames/sec) video cameras. Each resulting video frame shows the particles as white dots on a black background, like a starry sky. A sample frame is shown here from a 500 fps sequence.

From images such as these, the velocity field of the particles in this small region can be measured. Since there are three cameras, we can determine the full 3-dimensional velocity field in the small test volume at rates as high as 1000 Hz. We can then calculate the relevant physical quantity, the local energy dissipation per unit mass, ε.
The turbulent dissipation is calculated from a square norm of the shear matrix, (![]() ui /
ui /![]() xj):
xj):
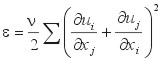 .
.
All past measurements of ε have been obtained from a one-component approximation of the dissipation:
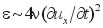 .
.
This new measurement will allow all calculation of all of the following quantities:
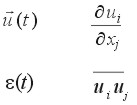 .
.
Theory and description of the experiment
Images of the current setup
 An image of the current setup.
All three laser beams and cameras are visible.
An image of the current setup.
All three laser beams and cameras are visible.
The tank is set up for convection in this picture.
Images of the turbulence experiment in a previous incarnation
Dissertations
- Benjamin Wolf Zeff, Three-dimensional dissipation scale measurements of turbulent flows, UMD 2002
Publications
- D.D. Lanterman, D.P. Lathrop, B.W. Zeff, R. McAllister, R. Roy and E. Kostelich. Characterizing intense rotation and dissipation in turbulent flows. Chaos. 14 (4): S8 (2004). [DOI] [ADS]
- T. van den Berg, C. Doering, D. Lohse and D. Lathrop. Smooth and rough boundaries in turbulent Taylor-Couette flow. Physical Review E. 68 (3) (2003). [DOI] [ADS]
- B.W. Zeff, D.D. Lanterman, R. McAllister, R. Roy, E.J. Kostelich and D.P. Lathrop. Measuring intense rotation and dissipation in turbulent flows. Nature. 421 (6919): 146-149 (2003). [PDF] [DOI] [ADS]
- E. Boettcher, J. Fineberg and D. Lathrop. Turbulence and Wave Breaking Effects on Air-Water Gas Exchange. Physical Review Letters. 85 (9): 2030-2033 (2000). [PDF] [DOI] [ADS]
- A. Juneja, D. Lathrop, K. Sreenivasan and G. Stolovitzky. Synthetic turbulence. Physical Review E. 49 (6): 5179-5194 (1994). [PDF] [DOI] [ADS]
- D. Lathrop, J. Fineberg and H. Swinney. Transition to shear-driven turbulence in Couette-Taylor flow. Physical Review A. 46 (10): 6390-6405 (1992). [PDF] [DOI] [ADS]







